Schatten, Schaal, Kijklijnen en Diagonaalvlakken

Tante besluit een wandeling in de natuur te gaan maken. Ze heeft een kaart met een schaal van 1: 15000 Op de kaart is de te lopen route 22 cm lang . In werkelijkheid is de route dus [?] km.

Bij het eindpunt staat een groot informatiebord. Daar ziet tante dat de kortste route naar een restaurant 2,4 km is. Op de kaart van tante is de route dus [?] cm lang.
Niet het hele gebied staat bij tante op de kaart dus koopt ze bij het restaurant een nieuwe kaart.
De volgende wandeling die zij maakt is wel 4,5 km lang. Op de nieuwe kaart meet ze een afstand van 9 cm. De schaal van de nieuwe kaart is dus [?] .

Kwik Kwek en Kwak staan voor een gebouw met 22 verdiepingen. Kwik zegt dat dit gebouw ongeveer 40 meter hoog is, Kwek zegt dat het ongeveer 65 meter hoog is terwijl Kwak zegt dat het 90 meter hoog is. Jij weet natuurlijk dat [?] gelijk heeft.

Blauwe Bram en Rooie Rinus racen door de stad op hun scooter. Zie onderstaande tekening.

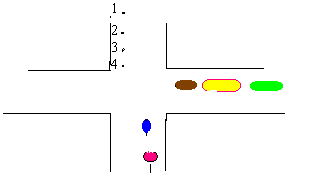
Uit de zijstraat komen een bruine, gele en een groene auto.
Blauwe Bram kan nog net de auto zien rijden. Rooie Rinus ziet nog net de auto.
Vanuit de bruine auto kan de chauffeur aan de andere kant punt [?] net niet meer zien.

In de onderstaande figuur zie je een bovenaanzicht van een bouwerk van blokjes. Op iedere positie staat aangegeven hoeveel blokjes er op elkaar gestapeld zijn.

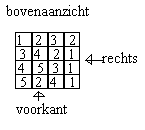
Als je het vooraanzicht bekijkt dan zie je (van links naar rechts) blokjes, blokjes, blokjes en blokjes.
Bekijk je het rechteraanzicht dan zie je het patroon 5 blokjes, 5 blokjes, 4 blokjes en 3 blokjes.
Als je het rechteraanzicht zo wilt veranderen dat het patroon 5, 3, 2 en 2 blokjes wordt moet je minstens [?] blokjes weghalen.

In de Balk in de onderstaande figuur is een diagonaalvlak getekend.

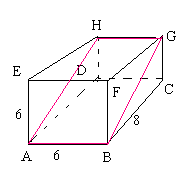
De lengte van diagonaal BG is [?].
De oppervlakte van dit diagonaalvlak (ABGH) is 60.
Van diagonaalvlak BCHE is de kortste zijde [?] (afronden op 1 decimaal) en de langste zijde [?] (afronden op 1 decimaal).

In een andere balk (zie figuur hieronder) is het vlak CGQR getekend.

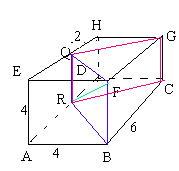
De lengte van GQ is [?] (afronden op 1 decimaal). De oppervlakte van CGQR is [?] (afronden op helen).
In het diagonaalvlak BFQR heeft de zijde FQ een lengte van [?] (afronden op 1 decimaal).
De zijde BF (=RQ) = [?] (afronden op helen).
De zijde RF heeft een lengte van [?] (afronden op 1 decimaal).